Relationship to other projects/themes
WP 1.2 has strong interlink with WP 4.1 and WP 3.1. It is using the concepts of normal form transformation from a data based approach. WP 1.3 on validation and ontologies has strong linkages to the Theme 0 work on classification.
Aims
To manage uncertainty in modelling and identification in both model structures and parameters and in anticipated future loading.
Progress to date
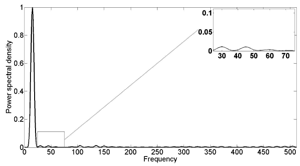
Figure 1: Power spectral density for transformed variable for the wind turbine blade shown in Theme 0 (Figure 1) at 15 Hz harmonic excitation
WP1.2 is concerned with prediction under uncertainty. As discussed under WP1.1, the system identification (SI) methodology developed there allows prediction under uncertainty to be carried out using Monte Carlo simulation.
While this is a general procedure, it can be computationally expensive, so the focus of WP1.2 so far has been on transformation of MDOF predictive models into simpler forms that facilitate computation. This began with a proposal for a data-based approach to nonlinear modal analysis, but evolved into a much more general framework, that of optimisation-based simplifying transformations.
The idea is to use optimisation to learn transformations of the physical coordinates to domains where the dynamics is simpler in some sense. If the objective is to obtain statistically independent responses under random excitation, the procedure allows a form of nonlinear modal analysis (and will be the subject of an invited paper in MSSP).
Variants of the algorithm have been developed using both polynomial transformations (which offer the possibility of physical interpretation) and nonparametric transformations derived using modern machine learning methods (kernel independent component analysis and nonlinear manifold learning).
The method can also deal directly with the output-only formulation of modal analysis. The nonlinear manifold learning analysis has proved powerful in the data-based approach to structural health monitoring (SHM), potentially solving the problem of when benign operational and environmental variations of the structure can lead to false alarms and mask the presence of damage. When the simplifying transformation is used in order to remove harmonic components in the response, one arrives at a form of data-based normal form analysis.

Figure 2: Nonlinear three-story building structure.
The research so far has developed the optimisation strategy, explored the effects of the transformation on unfiltered harmonics and also carried out an analysis of experimental data from the wind turbine demonstrator structure. Figure 1 shows a response from the turbine which has been ‘linearised’ by the transformation in the sense that the second and third harmonics have been removed. Because the simplifying transformations include nonlinear modal analysis and normal forms as ‘sub-theories’, they directly address problems from Theme 3. The successes in WPs 1.1 and 1.2 allowed an early start on the problems of WP1.3, which are concerned with Verification and Validation (V&V). V&V determines the degree of confidence in simulated models representing real structures and deals with concepts concerning the model fidelity-to-data, uncertainty quantification and the design of appropriate comparative metrics.
In the context of nonlinear systems, additional care must be taken in order to evaluate the examined models because of the bifurcations that may occur. The first goal of this work was to develop a model validation based on novelty detection. Datasets obtained from simulations of weakly nonlinear, chaotic and hyperchaotic systems are being used for the purpose as well as experimental data.
To support the analysis, the first objective was to develop a versatile and challenging test structure, and a variant of the Los Alamos National Laboratory ‘bookshelf’ structure (Figure 2) was designed and constructed. Initial work has been carried out based on a self-adaptive differential evolution algorithm, which has successfully identified a computational model. The structure has also provided test data form the MCMC algorithms developed in WP1.1.
As a result of synergy with a Leverhulme grant held in the Dynamics Research Group, it was possible to solve some of the sensitivity analysis problems initially reserved for WP1.3. This led to a windfall opportunity to explore a totally new concept for V&V, unforeseen at the programme proposal stage – that of the ontology. Making optimal decisions concerning V&V methodologies is critical in order to achieve cost-effectiveness, reliability and confidence.
Ontologies are widely used in knowledge engineering, semantics and computer science to codify domain knowledge and optimise information sharing; they allow the potential to develop ‘super expert systems’ for V&V, advising on test strategies and optimising them at the same time. The potential of ontologies has also been recognised as a means of generalising the planned ‘field guide’ for nonlinear SI. Furthermore, the concept can also be used as a means of implementing a new, population-based paradigm for SHM. Ontologies can be designed within specific software environments, like Protege; the learning curve is very steep, and an initial V&V ontology has been constructed.