Relationship to other projects/themes
This WP has developed very strong links with WP 2.2. This has led to one of the most significant research outcomes of the project to date on friction. There are also links to WP 1.1 on identifying systems with friction present.
Aims
To model vibration based systems with harsh nonlinear effects such as impact and friction using nonsmooth mechanics.
Progress to date
Progress has been in three areas:
Transient and frequency responses of frictional sliding.
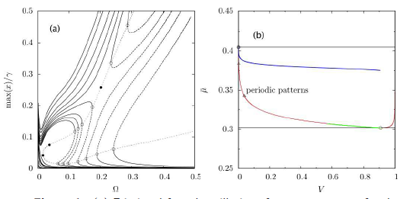
Figure 1: (a) Frictional forced oscillations frequency reponse for the spinodal RSF model. (b) Map of the frictional sliding modes of a thin elastic layer sheared. Symbols for the Hopf (red line), saddle-node (black line), slip (resp. stick) pulse homoclinic orbit loci (blue (resp. green) line); Bifurcation points: Bogdanov-Takens (◦), Bautin generalized Hopf (△).
The development and experimental identification of new rate-and-state friction models (RSF) has been studied. In particular the determination of the state evolution equation that governs the relaxation of the internal state variable measuring the resistance to slip of a frictional interface, has been studied from revisiting pioneering work such as the Rabinowicz frictional sliding block experiment and the Den Hartog frictional forced vibration experiment.
We have established how the RSF models can explain the Rabinowicz persistence length characterising the slip distance required for friction to drop from its static to its dynamic value, hence bridging the gap between the static and dynamic concepts of friction. The work also highlights that RSF models produce complex sub-resonance frequency responses very different from nonsmooth Coulomb friction, in particular the existence of bistability domains in which large amplitude periodic orbits co-exist with very small amplitude orbits characterised by nano/microslippage (Figure 1(a)).
The use of Bayesian identification techniques to study whether RSF models can be identified using frictional forced oscillations has been exploited in collaboration with the Sheffield team (Green, Lord WP1.1). This is an area of work we will develop in the future.
Friction slip localisation (MS7)
Inhomogeneous frictional sliding between solid bodies is ubiquitous, ranging from earthquakes to vehicle brake squeal, and is typically characterised by multiple spatio-temporal scales. The understanding of the physical mechanisms that determine the diversity of the frictional slip pattern formation that has been reported over the years relies in part on the modelling of the friction phenomenon.
Depending on non-monotonic (N-shape) RSF models and applied to a thin elastic slab configuration, we have made significant advances regarding the spatiotemporal nonlinear dynamics of frictional ruptures, noticeably with regards to the occurrence of frictional travelling self-healing slip pulses, which we show to arise from a homoclinic global bifurcation of travelling periodic slip patterns (Figure 1(b)). Numerical continuation also uncovers the possibility of ‘stick pulse’ travelling along a thin elastic layer sliding fast.
Mechanics of the pin-on-disc friction rig (MS11)
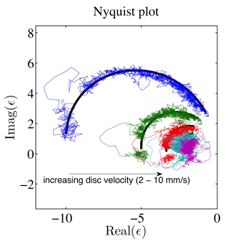
Figure 2: Nyquist plot of the dynamic frictional impedance ϵ(ω) ≡ F′/(v′N): experiment (coloured traces), theory (thick black line). F′ and v′ denote the fluctuations of the friction force and the contact slip rate.
The pin-on-disc experiment developed in Cambridge (Woodhouse & Cabboi) is described under Theme 2, WP 2.2. Recent efforts to combine RSF models with the effect of an effective tangential contact/interfacial stiffness, confer- Figure 2: Nyquist plot of the dynamic frictional impedance ϵ(ω) ≡ F′/(v′N): experiment (coloured traces), theory (thick black line). F′ and v′ denote the fluctuations of the friction force and the contact slip rate. ring a frictional interface with some Maxwell viscoelastic properties, are showing remarkably good agreement in reproducing qualitatively and quantitatively the experimental observations (Figure 2).
In addition the PhD work of MacKay (WP2 co-supervised by Putelat) regarding the definition of various experimental metrics for discriminating friction models will be highly complementary to this work. Overall, these new results open scope of major advances in the physics of friction and for the experimental identification of reliable dynamic friction models over a wide window of friction environments and the possibility of industrial implementation of this experimental protocol. (iv) Weak formulation of contact problems.
Work by associated academic Robert Szalai and PhD student Yani Berdini have considered a new formalism that can exactly describe the dynamics of point contact by transforming the partial differential equations of a continuum into a delay differential equation with low number of variables. The variables described by the equivalent delay equation include the positions and velocities of the contact points, hence it is ideal to couple these equations with contact laws such as friction and collision.
The exact nature of friction laws was not part of this analysis, although this is planned to be a continuation of the work of Putelat. The immediate consequence of the new formalism is that by including all the dynamics it regularises commonly used approximate low order models: friction force is now a continuous function of time and contact forces during collision is now finite, as well.
Collisions can now be better modelled, because they take finite time and do not require impulsive forces (if wave speeds in the underlying structure are finite). The new formalism is currently being generalised to contact problems of weakly nonlinear structures and to extended contact problems.
Another future line of enquiry deals with identifying the reduced model from experimental data.